In the above continued fraction, replace the letters a,b,c,d with the numbers 1,4,5,7 in whatever order you wish.
What is the maximum value of x?
Your Custom Text Here

In the above continued fraction, replace the letters a,b,c,d with the numbers 1,4,5,7 in whatever order you wish.
What is the maximum value of x?
The following words all have something specific in common:
SCAR THOU NAPA SOLE TECH DOLL DIVE DIVE GALA
The order they are in is related to the thing they have in common.
DIVE is in the list twice – this is not a mistake.
Which one of the following words also belongs in the list, and where in the list should it be placed?
BECK CLEF PARA PAST
If 32 degrees Fahrenheit = 0 degrees Celsius,
and -40 degrees Fahrenheit = -40 degrees Celsius,
calculate in your head what temperature will be the exact same amount of degrees for each but positive for Fahrenheit and negative for Celsius.
Some quarter circles (and semi circles) are arranged in (and out) of a rectangle as shown. What is the length of the line marked with a question mark?

What number is missing from this sequence?
11, 236, 315, 4384, 5175, ???, 7735, 8128, 9135,
I’ve started with a 3x3 square, and divided it into 9 1x1 squares as shown. I’ve added four 1x1 squares such that for each of them one corner lies on a corner of the central 1x1 square, and the corner opposite that lies outside of the 3x3 square. I’ve used this as the basis of the lower figure, a bizarre 20 sided polygon.
What is the perimeter of this polygon?

A straight line is drawn through a circular array as shown. The line is tangent to the lower left and upper right circles. This line passes through some of the other circles and also passes through the space between the circles.
What proportion of the line is within the circles?

A player plays a Wordle type game, where feedback is given after each guess. The player correctly finds the answer ‘DELAY’ on her fourth guess. Her guesses were:
I S S U E
A L A R M
B I D E T
D E L A Y
At each point the guess could have been the solution, in other words she hasn’t employed any clever elimination tactics. There were still a handful of other possibilities at the point where she got the answer, but it was not unreasonable that she guessed it after four guesses given the feedback she had.
What feedback was she receiving after each guess?
An extra challenge if you fancy it: find another word that still might have been the answer after the first three guesses, with the feedback as it would have been for DELAY.

Still on the subject of kites, it is straightforward to dissect a regular pentagon into five identical kites as shown. If the kites all need to be different however, as far as I can tell you need at least 7 kites to make up a regular pentagon. But how might you do it?
We are using the definition that kites must be convex, with two pairs of identical sides located adjacently (as opposed to a parallelogram where the identical sides are opposite). A hint: a rhombus is allowed as a special case of a kite.
It is possible to dissect ANY non-square rectangle into one square and four DIFFERENT non-square kites. How?
(A kite is defined as a quadrilateral with two pairs of identical sides, with the identical sides adjacent – unlike a rectangle where the identical sides are opposite).
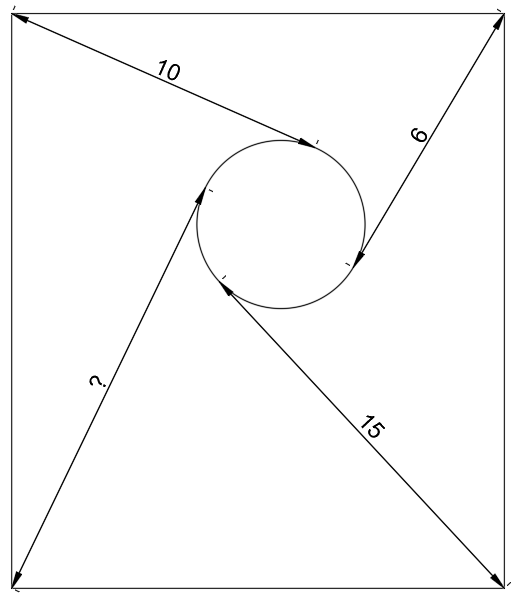
Lines are drawn from each corner of a rectangle, tangent to a circle as shown. The lengths of three of these lines are 10, 6 and 15. What is the length of the fourth line?
Joshua and Leoni have been next-door neighbours for the past 34 years
In 1990, Joshua’s age was the sum of the digits of Leoni’s age.
In 2024, Joshua’s age is the sum of the SQUARES of the digits of Leoni’s age.
How old were they and are they?
Eight unit squares are placed within a right-angled isosceles triangle as shown.
What is the area of the triangle?

This is my portable smartphone USB-C charger. It very handily and neatly docks onto the charging port of my android phone, without any need for a wire between them. To charge the charger there is a socket on the end as shown, which is also USB-C.
My question is, if you had a supply of chargers identical to this one, how many would you need to form a ring, where each charger was charging the next one in the chain?

Within a rectangle of area 882, a square of area 196 is drawn, aligned with the corner of the rectangle, and tangent to the diagonal of the rectangle as shown.
A second square is drawn, aligned to the diagonal, and tangent to the outside of the rectangle as shown. What is the area of this sloping square?

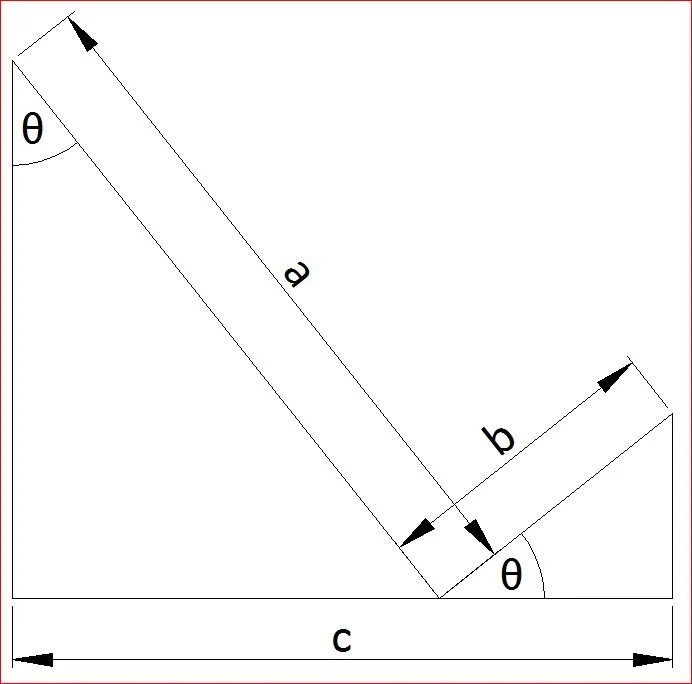
Θ is an acute angle
a(sin(θ)) + b(cos(θ)) = c
If you know a, b and c, how can you calculate θ ?
A right-angled triangle has a height of 4, and one its sides is 3 more than another as shown. What is the length of the base?

Cut out a heptagonal ‘bite’ from a circle. The bite is four sides of a regular heptagon. The remaining arc length should be constant, and you wish to maximise the area. Below are two figures towards the extremes: a small circle with a small heptagon bite, or a far larger circle, but where the heptagon takes most of that area. In between these two figures there will be a point where the area is at a maximum, but how to construct it?

I had previously solved a far simpler version of this, where the bite was formed by two edges of a square. The optimum in that situation was for the inner vertex of the square to lie on the centre of the circle. In other words the resulting figure would be a three-quarter-circle. It turned out on further examination that the fact that the two lines of the square met at right angles was not important, but the fact that the lines were equal WAS. So if the bite was formed of two identical lines meeting at ANY angle, the maximum area for that angle is achieved when the vertex lies on the centre of the circle:

How can you use this information to construct the maximum area in the case of the heptagon?
I have 7 copies each of 14 cards labelled A-N. Each day I try to play a card. I cannot play the same letter as the previous day. In addition if I played a letter for the nth time, the next day I cannot play another letter for the nth time. If I cannot play a card I must take a day off, but the following day I can play whatever card I want.
How many days will it take me to play all of the cards?
Within this right-angled triangle a rectangle is drawn. Four identical blue circles and two identical red circles are drawn, tangent to each other, the rectangle and the triangle as shown. If the radius of the red circles is 9, what is the radius of the blue circles?
