A rectangular block measuring 375cm x 200cm is positioned in a 340cm wide alleyway as shown. How much higher is the left corner than the right?
Puzzle of the Week # 341 - Mastermind
A code of three coloured pegs is selected from Red, Yellow, Green, Orange, Blue and Purple.
Guess 1: Red Yellow Green: one correct but in the wrong position
Guess 2: Orange Blue Purple: one correct but in the wrong position
Guess 3: Red Red Purple: one correct, and in the correct position
Solution: ?
Puzzle of the Week #340 - Infinite Coin Push
We used to play a game back when I was at school. We would start with three coins placed widely apart on a table. The first player would give one of the coins a shove, so that it would pass between the other two. Then the next player would try to do the same, starting from the current position, but using one of the other coins. This would continue until one player would inevitably fail to get the coin between the other two.
I’m now imagining an idealised version, where the coins are single points, and on each turn the coin passes through the exact midpoint of the positions of the other two coins and continues a further 50%. So to begin with, the coins are at (0,0) (3,9) and (9,3) respectively. The midpoint of the initial positions of coins B and C is clearly at (6,6), so coin A will travel from (0,0) to (6,6) and then continue another 50% to come to rest at (9,9). Next it is the turn of coin B. Coin B must travel to the current midpoint of coins A and C and extend another 50% distance to find its new position. The coins take turns in the order A, B, C, A, B, C etc
The diagram below shows the first two moves of each coin.
After an infinite number of moves, where will each of the three coins be?
Puzzle of the Week #339 - Envelope Centroid
ABC is an equilateral triangle. If I tell you that the area of the unshaded region is sqrt(3)/6 and that the centroid (centre of gravity) of the unshaded region is sqrt(3)/10 above AC, how far above AC is the centroid of the shaded region?
Puzzle of the Week #338 - Base 4 Riddle
I have taken a riddle, and I have replaced each of the letters with the numbers that denote their position in the alphabet. However, I have used the base 4 number system.
Be careful, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10). Can you decode the riddle and then solve it?
21'31 12331113210 2132 10333323103, 1033110211211103 13210 31211101101132103; 13210 33121101132 2132 1102011 1001113103 3312 1003011211211130 23211101101132103. 113201110 131 21?
Puzzle of the Week #337 - Unit Square
Three straight lines are drawn in a 1 x 1 square as shown, such that one line extends between opposite corners, and the other two line meet at one of the other corners, with the other end of each line meeting the edge of the square partway along an edge.
What is the maximum possible combined area of the shaded regions?
Puzzle of the Week #336 - Consecutive Missing Letters
The missing letters in each of the following words are found next to each other in the alphabet. The missing letters might or might not be repeated amongst the missing letters, for instance _ _ _ _ _ G E could be CABBAGE, since A B and C are to be found together in the alphabet.
Complete each of the following words using a set of five alphabetically consecutive letters in each case. Each uses a different set of five letters, but there may be some overlap.
_ L _ M _ _ R _ _
_ _ R _ _ _ _ _ T _ R
_ E _ _ E _ _
Puzzle of the Week #335 - Maximum Quotient
Take a five-digit-number and split it at some point between the digits into two shorter numbers (for instance 12345 could be split into 123 and 45), then multiply together the two shorter numbers. Take your original five-digit-number and divide by this product.
In our example this quotient would be 12345 / (123 x 45) = 2.23…
What is the highest this quotient can be, and what is the five-digit-number that achieves it?
Note: each of the two shorter numbers must start with a non-zero digit, so 12003 could split into 1 and 2003, or 1200 and 3, but not 12 x 003.
Puzzle of the Week #334 - Skeleton Cube
I have taken a unit cube and removed any material that coincides with a unit radius sphere centred on one of the vertices, then I have removed any material that coincides with another unit radius sphere centred on the opposite vertex. This has resulted in a circular hole in the middle of what is left of the cube. What is the diameter of this circular hole?
Puzzle of the Week #333 - Non-seqitur
Attempt this question without any electronic assistance.
Given that the square root of 10 is about 3.16,
how many 5- or 6-digit number are there with exactly 5 factors (including 1 and itself)?
Puzzle of the Week #332 - Even Binary Puzzle
Consider a process by which you take a binary number with an even number of 1s, (for instance 92 = 1011100 has 4 1s), chop the number into two chunks such that each chunk has the same number of 1s, and each chunk begins with 1 (101=5 and 1100=12). Then multiply these two numbers together to give a number smaller than the one you started with (111100=60). If the new number has an even number of 1s, repeat the process, otherwise stop. (11=3 and 1100=12 gives 100100=36; 100=4 and 100=4 gives 10000=16; stop).
25 and 32 both convert to binary numbers with an odd number of 1s, (11001 and 100000 respectively).
What is the highest number that will eventually terminate in at 25?
As a bonus question, what is the highest number that will eventually terminate at 32?
Puzzle of the Week #331 - Sixth Powers
All square numbers are either a multiple of 5 or one away from a multiple of 5. 5 is the highest number for which this is true.
For cube numbers, the highest number that every cube number is at most one away from a multiple of, is 9.
What is the highest number for which it is true that every sixth power (1, 64, 729, 4096, etc) is at most one away from?
Puzzle of the Week #330 - Self-Assembly
Assemble these two- and three-letter chunks into six surnames of famous people with a specific occupation in common:
ANE BO CH CHA ER ETT
HA ILL LL MM NDE NDL
NES RE RIS SP TIE
Puzzle of the Week #329 - p+2=sp
I have a number, n, for which it is true that whenever a semiprime is 2 greater than a prime, they are either both factors of n, or neither are. A semiprime is a number with exactly two prime factors, for example 4 (2x2) or 6 (2x3).
So for instance, 33 is a semiprime (3x11) which is 2 greater than a prime (31), and so EITHER 33 and 31 both divide into n, OR neither do.
My number only has one pair of repeated prime factors: a pair of 3s. All its other prime factors are unique.
n is the smallest possible number to satisfy the above rules. What is n?
For an extra challenge, what is the next smallest number that satisfies the rules?
Puzzle of the Week #328 - Binary Determination
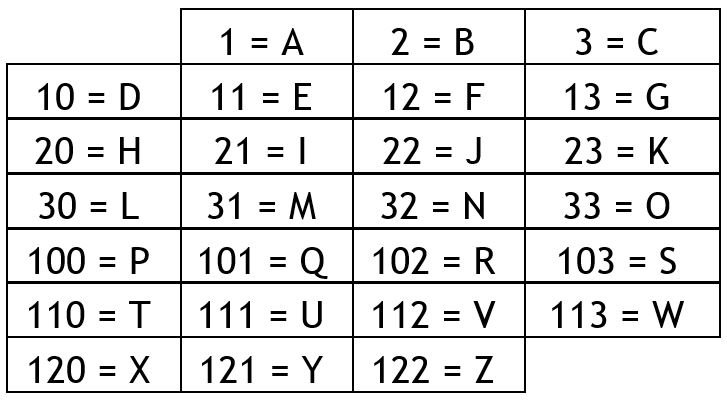
Place either a 0 or a 1 in each empty square such that each row and each column will form a correct multiplication of two binary numbers to give the decimal number at the end of the row or column. For instance, if the product is 12, the row might read 011x100 (3x4), or one of a number of other possible combinations. I have provided decimal-to-binary tables to help you. Here are two puzzles, one with binary numbers of up to three digits, and one up to four digits.
Puzzle of the Week #327 - False Conjecture
The sequence: 1, 21, 321, 4321, etc is very simple to generate. It is the sum of k(10^(k-1)) for all k between 1 and n, with the results of n=1, 2, 3, 4 shown above. It only gets slightly messier when n is in double digits, for instance the 14th number in the sequence is: 14320987654321, and the 28th number is 30987654320987654320987654321.
It was conjectured that no number in this sequence is prime, but that turns out to be false.
Can you find the first counterexample? Just to warn you this cannot be done without a computer.
Puzzle of the Week #326 - Inch Centimetre Prime
I am thinking of a distance, less than 200m, which is an exact whole number of inches and also an exact whole number of centimetres (one inch is precisely 2.54cm).
The number of inches is one more than a prime number.
The number of centimetres is one more than a prime number.
The sum of the number of inches and the number of centimetres is also one more than a prime number.
What is the distance?
Puzzle of the Week #325 - Uprooted
If (x times the square root of y), plus (y times the square root of x) is 14,
and (x times the square root of x), plus (y times the square root of y) is 22
What is the value of (x plus y)?
Puzzle of the Week #324 - Number Hunt
Can you find a seven-digit number containing seven different digits, whose prime factors are four two-digit primes containing between them eight different digits?
Puzzle of the Week #323 - Triangle Rectangle 2
This is quite similar to PotW #320 but differs in a couple of respects. Firstly, the rectangle is a slightly different height. Secondly, the point F no longer needs to lie on CD, but is free to be anywhere, subject to the other conditions (that ABCD is a rectangle, AEF is a right angle, and E lies on BC.
What is the minimum that DF could be?