Your Custom Text Here
This is my portable smartphone USB-C charger. It very handily and neatly docks onto the charging port of my android phone, without any need for a wire between them. To charge the charger there is a socket on the end as shown, which is also USB-C.
My question is, if you had a supply of chargers identical to this one, how many would you need to form a ring, where each charger was charging the next one in the chain?
Within a rectangle of area 882, a square of area 196 is drawn, aligned with the corner of the rectangle, and tangent to the diagonal of the rectangle as shown.
A second square is drawn, aligned to the diagonal, and tangent to the outside of the rectangle as shown. What is the area of this sloping square?
Θ is an acute angle
a(sin(θ)) + b(cos(θ)) = c
If you know a, b and c, how can you calculate θ ?
A right-angled triangle has a height of 4, and one its sides is 3 more than another as shown. What is the length of the base?
Cut out a heptagonal ‘bite’ from a circle. The bite is four sides of a regular heptagon. The remaining arc length should be constant, and you wish to maximise the area. Below are two figures towards the extremes: a small circle with a small heptagon bite, or a far larger circle, but where the heptagon takes most of that area. In between these two figures there will be a point where the area is at a maximum, but how to construct it?
I had previously solved a far simpler version of this, where the bite was formed by two edges of a square. The optimum in that situation was for the inner vertex of the square to lie on the centre of the circle. In other words the resulting figure would be a three-quarter-circle. It turned out on further examination that the fact that the two lines of the square met at right angles was not important, but the fact that the lines were equal WAS. So if the bite was formed of two identical lines meeting at ANY angle, the maximum area for that angle is achieved when the vertex lies on the centre of the circle:
How can you use this information to construct the maximum area in the case of the heptagon?
I have 7 copies each of 14 cards labelled A-N. Each day I try to play a card. I cannot play the same letter as the previous day. In addition if I played a letter for the nth time, the next day I cannot play another letter for the nth time. If I cannot play a card I must take a day off, but the following day I can play whatever card I want.
How many days will it take me to play all of the cards?
Within this right-angled triangle a rectangle is drawn. Four identical blue circles and two identical red circles are drawn, tangent to each other, the rectangle and the triangle as shown. If the radius of the red circles is 9, what is the radius of the blue circles?
Solve these clues and place the answers in the correct order:
Santa’s little helper
Long term prisoner
Dossier
Lightning bug
Interleaf (playing cards)
Four circles are drawn in a unit square as shown. The two lower circles are the same size. What is the radius of the small circle, as a fraction?
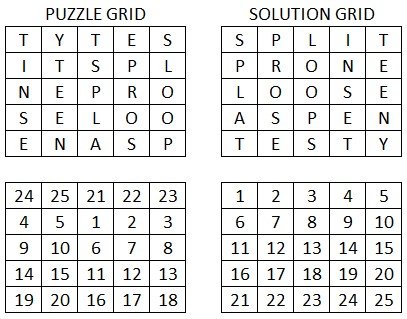
I have taken a square of five letter words and scrambled it in a particular way: each letter was moved across 2 and down 1 from its position in the solution grid, which is made clearer by the corresponding number grid below.
This is a logic puzzle, not a word puzzle, as is apparent from the fact that I’ve given you the solution grid as well as the puzzle grid.
Your task is to figure out the least number of swaps required to turn the puzzle grid into the solution grid, with each swap simply being to take any two letters from anywhere in the grid and swap them.
If you attempted this on the number grid, you would require 20 swaps, however in the letter grid you can take advantage of the fact that some letters are repeated to reduce the number of swaps.
A bonus question if you feel like it, is to work out how many swaps you can make that, while advancing towards to solution within the minimum number of swaps, don’t actually solve any letters. To explain what I mean, in the number grid if you were to swap the 1 and the 15, neither would be in its final position, but you have advanced the solution in the sense that it can now be solved in 19 further swaps.
What is the value of:
The following list of words are in alphabetical order. Change them into a different order that also has some reason behind it but has nothing to do with the alphabet.
Antenna
Freighter
Lioness
Network
Zaniness
****Thank you for trying to solve my puzzles this year. This is the last for 2023 as I take a break over the Christmas period. I’ll be back in the new year.****
Here is a pentagon with five equal sides, however its angles are not all equal. Two of them are right angles as shown. Can you dissect this pentagon into just three pieces and reassemble them to form a square?
2*f(3/(3-x)) – f(x) = 135*x
What is the value of f(4)?
f(x) is a function of x. The above is a ‘functional equation’, where f() of more than one different value appears as an unknown. It may look intimidating, but if you approach it in the right way, it is solvable without any advanced mathematics. As a slight push in the right direction, see what happens if you let x=4.
In this grid, each number needs to be the sum of the two numbers immediately below. Once complete, the bottom row will spell out a famous date in English history.
There is only one real value which satisfies this equation, what is it?
(2x+3)(3x+4)(4x+5)=11
A triangle DEF sits atop a 24 x 24 square ABCD. The triangle is special for a couple of reasons. E D and C are collinear, and E F and B are also collinear. In addition, the area of triangle DEF has the same value as its perimeter. What is that area?
It is possible to write the numbers 1 to 441 in a particular order such that the sum of every consecutive pair of numbers is either 321, 442, or 763. For instance, 400 might be followed by 42 or 363.
When you do this, what numbers are at the start and the end of the sequence?
And for bonus points, what number would be in the exact centre of the sequence?
This is a regular hexagon with unit length sides. The radius Ra is obviously equal to 0.5, but the other radii are all different. What is the value of radius Re?
The numbers p, q, r and s are odd prime numbers such that:
p+5 is divisible by q
q+6 is divisible by r
r+7 is divisible by s
s+8 is divisible by p
What are p, q, r and s?