If the triangle has base 5 and height 2, then it will have hypotenuse of square root of 29. The smaller copies will therefore have hypotenuse of 1 and can fit together as below:
Solution of the Week #422 - Boggle E
Badge, bead, beck, café, code, complied, deaf, deck, face, faced, fade, gecko, head, heck, lied, life, mode.
Solution of the Week #421 - Odd Prime Balance
The lowest solution is achieved when T is 6 and U is 24. To find the values of V to Z, just choose the lowest number for which p, p+6 and p+24 are all prime, then the next lowest without overlapping, etc. So, our V to Z are 5, 7, 17, 37 and 47.
Our A to O will then be:
A = 5
B = 7+6 = 13
C = 17+24 = 41
D = 37
E = 47+6 = 53
F = 5+24 = 29
G = 7
H = 17+6 = 23
I = 37+24 = 61
J = 47
K = 5+6 = 11
L = 7+24 = 31
M = 17
N = 37+6 = 43
O = 47+24 = 71
Giving a total of 489, using 15 of the first 20 prime numbers.
Thanks to Graham Holmes for finding this optimal solution.
Solution of the Week #420 - Fourth Powers and Fourth Fractions
The initial step is to try to find a useful factorisation of the general form (n^4 + 1/4).
We will aim to factorise into two factors as below:
(n^2 +mn +1/2)(n^2 –mn +1/2)
Clearly the first terms in each bracket will combine to give the sought after n^4, and the last in each bracket will give the 1/4 we need. The fact that we have +mn and -mn means that the n^3 terms will cancel, as will the n^1 terms. We must then choose a value of m such that the n^2 terms disappear too.
Just showing the n^2 terms, we have (1/2)n^2 +(1/2)n^2 =(m^2)n^2.
m^2 = 1. So m is +/-1 (but since we have +m in one bracket and -m in the other it makes no difference which we choose).
So (n^4 + 1/4) = (n^2 +n +1/2)(n^2 -n +1/2)
We still need some further manipulation before it becomes useful.
If we take the first bracket and rewrite it as:
(n^2 +n +1/4 +1/4)
Then the first three terms form a perfect square:
((n+(1/2))^2 +1/4)
Doing the same for the second bracket we get
((n-(1/2))^2 +1/4)
To see how this is useful, let’s rewrite some of the terms of the initial question in this new form:
(1^4 +1/4) = ((1.5)^2 +1/4)((0.5)^2 +1/4)
(2^4 +1/4) = ((2.5)^2 +1/4)((1.5)^2 +1/4)
(3^4 +1/4) = ((3.5)^2 +1/4)((2.5)^2 +1/4)
The term ((1.5)^2 +1/4) will appear once in the numerator and once in the denominator, and so will cancel out. This will be true for almost all of the terms in the expression and we will just be left with: ((10.5)^2 +1/4)/((0.5)^2 +1/4)
To aid mental calculation, we can rewrite these two terms in the previous form:
(10^2 +10 +1/2)/(0^2 +0 +1/2)
110.5 *2
And so the solution is precisely 221.
Solution of the Week #419 - Minimum Triangle
It is tempting to think that the triangle would need to be Pythagorean. Certainly for any Pythagorean triangle, the values of a and b would be whole numbers, and c would be a rational number. Suitably scaled up, this too can become a whole number. For instance, if we started with a 3-4-5 triangle, a would be 2 and b would be 3. c would work out to be 2.4. Scaling everything by 5 would give a solution of (10,15,12) with a total of 37. This is not however the minimum solution.
It's a nice little fact that the area of such a triangle is simply a*b. It’s simple enough to prove with a bit of algebra; I’ll leave it to the reader to try it. And if you find a nice geometric proof, let me know as thus far one has eluded me!
That being the case, (a+b)*c/2, the standard way of finding the area, must be equal to a*b. Rearranging, we need to find two numbers a and b such that their product divided by their sum is either a whole number or a half number. The first such pair is 2 and 6, yielding the minimum solution of (2,6,3). The area is 12, which is both 2*6 and (2+6)*3/2. So the answer is 11. The resulting triangle is certainly not Pythagorean, having sides (2*sqrt(7)-2, 2*sqrt(7)+2,8).
Solution of the Week #418 - Fourth Circle
Because three of the circles are tangent at the same point, their centres lie on a straight line. That being the case, if we draw lines connecting all of the circle centres, we can form two triangles which both use the angle ‘x’: the 90,120,70 triangle and the (R+70),120,R triangle.
We can use the law of cosines which states:
Cos(a) = (B^2+C^2-A^2)/(2BC), (where side A is opposite angle a)
If we do so first for the 90,120,70 triangle, we find that cos(x) = 22/27.
Now if we do the same for the large triangle, we already know cos(x), so:
22/27 = (140R + 19300)/(240R + 16800)
22(240R + 16800) = 27(140R + 19300)
1500R = 151500
R = 101
So therefore the radius of the fourth circle is 101.
Solution of the Week #417 - Triple Duality
ERA, ATTEND, BISHOP, DEW, TOLERABLE, END, BLEMISHES, BISMILLAH, MILDEW, ADVICE, MISFIT, ARC, ADVERB, HOP, ATTACK, AYATOLLAH, PAPERBACK, FIT, PAPAYA, ARCHES, ICE.
Solution of the Week #416 - 2023 Rectangle Ratio
The first thing to notice is that the area given for the square is not a square number. Since ultimately we are only interested in the ratio of sides of the rectangle, we should have no problem scaling up the figure so that it is. Since 3375 = 3^3 * 5^3, if we multiply this (and the rectangle area) by 15, we will get a square number. The side of the square will then be 225, and the new rectangle area will be 2023*15 = 30345.
The other dimensions in the figure below are related to one another by Pythagoras and similar triangles.
120 + 105 = 225
255 * 119 = 30345
225^2 + 120^2 = 255^2
255/225 = 119/105
Since all those are satisfied, these must be the correct dimensions. Therefore the ratio of the rectangle’s sides is 255/119, which is 15/7.
Solution of the Week #415 - Alchemy
There are probably several solutions, but the one I found is:
CARBON – ACORNS – REASON – ARISEN – SERIAL - SILVER
Solution of the Week #414 - Mystery Sequence
Each number is the lowest number that hasn’t yet appeared in the sequence, that begins with the last letter of the previous number.
ONE – EIGHT – TWO – ONE HUNDRED – DECILLION – NINE – ELEVEN – NINETEEN - NINETY
No numbers begin with ‘y’.
I realise I’ve been a little inconsistent with names of numbers, allowing 100 to be called ‘one hundred’ but 10^33 as merely ‘decillion’ not ‘one decillion’ but that was the only way!
Solution of the Week #413 - Interior Point
Since the lines meet the edges of the square at the midpoints, we can divide the square into pairs of triangles with identical areas as below.
From the puzzle a+b=33, c+d=39, therefore the entire square, 2(a+b+c+d)=144, so the square is 12x12 and the base length of each of the eight triangles is 6. Because it is a square we also know that the a and c triangles make up half the area, and the b and d triangles make up the other. So a+c=b+d=36.
With all of this information we can determine the values of the individual areas to be a=12, b=21, c=24, d=15.
Looking only at the areas a and d will pinpoint the coordinates of the interior point (4,5).
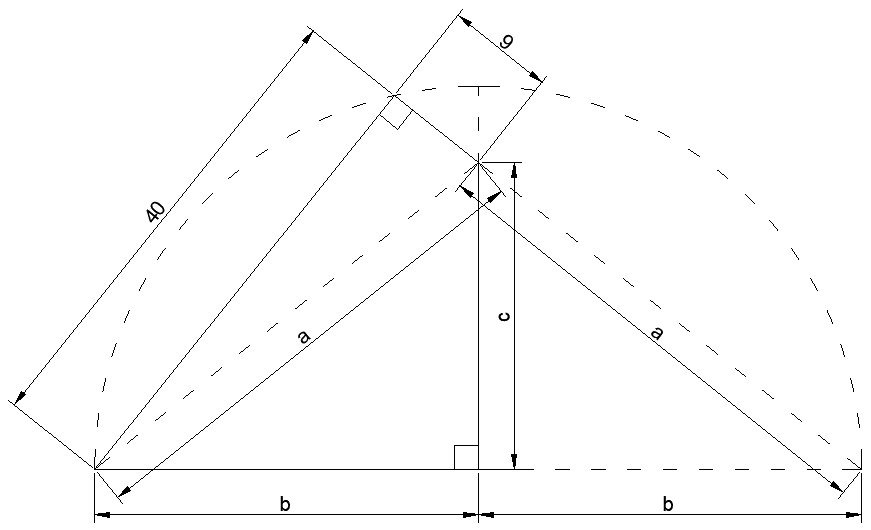
Solution of the Week #412 - Quad in a Quarter
From Pythagoras on the (40,9,a) triangle, the length of a is 41. If we reflect this in the vertical axis we get a line that is collinear to the line of length 9. This gives another right-angled triangle (40,9+a,2b) and using Pythagoras again we find b=5*sqrt(41). Using Pythagoras yet a third time on the (b,c,a) triangle, we find c=4*sqrt(41). Finally to find the area of the quadrilateral we calculate ((40*9)+(b*c))/2, which neatly cancels out the square roots and gives the answer of 590.
Alternatively, the following shortcut means you don’t even have to calculate b or c: notice that the quadrilateral exceeds the 40*9 triangle by the exact same amount that the 40*50 triangle exceeds the quadrilateral. So the quadrilateral will be the average of the areas of the 40*9 triangle and the 40*50 triangle, so (180+1000)/2 = 590.
Solution of the Week #411 - Best Remakes
Winner 1930, nominated 2022: All Quiet on the Western Front
Winner 1961, nominated 2021: West Side Story
Nominated 1933 and 2019: Little Women
Nominated 1937 and 2018: A Star Is Born
Nominated 1935 and 2012: Les Miserables
Nominated 1952 and 2001: Moulin Rouge
Nominated 1943 and 1978: Heaven Can Wait
Nominated 1936 and 1968: Romeo and Juliet
Nominated 1934 and 1963: Cleopatra
Winner 1935, nominated 1962: Mutiny on the Bounty
Solution of the Week #410 - Six Starfish
Solution of the Week #409 - Classes
If we say that class B has ‘x’ girls, and class C has ‘y’ boys, then class A has 2x girls and 4y boys. Also, we are told that class C has 2 more girls than class B has boys, but since the classes are equal that means class B has 2 more girls than class C has boys. So x = y+2. Class A has 2(y+2) girls and 4y boys, so 6y+2 students in total. Again since all classes are equally sized, class B has y+2 girls and therefore 5y+2 boys, and class C has y boys and therefore 5y+4 girls. In total there are 8y+10 girls and 10y+2 boys. Since we are told these numbers too should be equal, y=4.
Therefore class A has 12 girls and 16 boys, class B has 6 girls and 22 boys, and class C has 24 girls and 4 boys. There are 84 students in total.
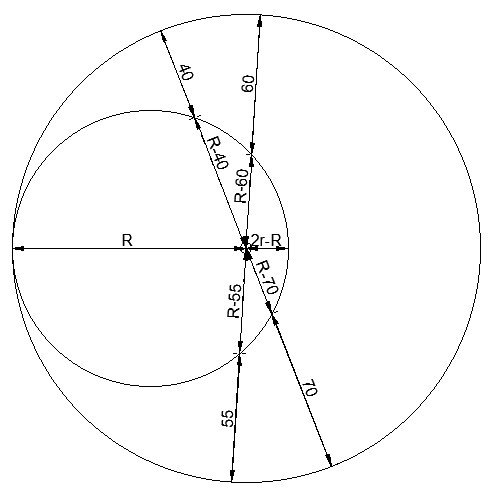
Solution of the Week #408 - Eclipse
If we call the radius of the large circle ‘R’ and that of the smaller circle ‘r’, then the shaded area is pi*(R^2-r^2).
To first determine R we look at the chords that cross the small circle, then will have lengths of (R-40), (R-60), (R-70) and (R-55). According to the intersecting chords theorem, the product of the opposite pairs will be equal.
(R-40)(R-70)=(R-60)(R-55)
R^2 – 110R + 2800 = R^2 - 115R + 3300
5R = 500
R=100
So each side of the equation (R-40)(R-70)=(R-60)(R-55) will be equal to 1800.
To find r, we can draw a third chord, which goes from the tangent point, and through both centres. The intersecting chords along this line will be R and 2r-R.
R(2r-R) = 1800
200r – 10000 = 1800
r – 50 = 9
r=59
100^2 – 59^2 = 6519. The shaded region is therefore 6519*pi, which is about 20480.
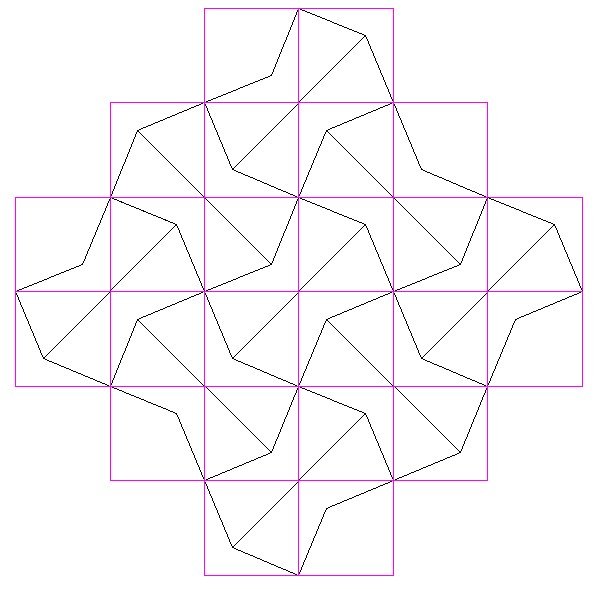
Solution of the Week #407 - Strange Area Dissection
It is possible for this shape to tile the infinite plane, if copies of the shape are rotated 45, 135, 225 and 315 degrees from the original. You can then overlay a unit square grid which neatly lines up with the shape as below:
Translating this back to the original shape, this corresponds to drawing lines from the centre of the semicircle to each of the 90 degree corners, dissecting the shape into two isosceles triangles and a dart shape. Not only is this a dissection in only three pieces, but it can be hinged as well, a la Henry Dudeney.
Solution of the Week #406 - Strange Area
Divide the shape into two areas as above. Because angles in a semicircle are right angles, the length marked ‘y’ is an extension of one of the ‘x’ edges, and exactly meets the bottom corner of the semicircle.
y is the hypotenuse of an isosceles right triangle whose legs are x, and so therefore y = x*sqrt(2).
Using Pythagoras on the large triangle we get that:
x^2+(x+y)^2 = 4
x^2+(x+x(sqrt(2))^2 = 4
x^2 + x^2 + 2(sqrt(2))x^2 + 2x^2 = 4
x^2 (4+2(sqrt(2)) = 4
x^2 = 4/(4+2sqrt(2)) = 2/(2+sqrt(2))
multiplying the right hand side by (2-sqrt(2))/(2-sqrt(2)) to eliminate the square root in the denominator:
x^2 = (4-2sqrt(2))/(4-2) = 2-sqrt(2)
The area of the two triangles will be respectively x(x+y)/2 and x^2/2, so the combined area is (2x^2+xy)/2. Since y=xsqrt(2), the area is: (x^2)*(2+sqrt(2)/2)
Replace x^2 with the known value of 2-sqrt(2):
(2-sqrt(2))*(2+sqrt(2))/2
(4-2)/2
1
Therefore the area of the shape is simply 1.
Solution of the Week #405 - Number Hunt
All prime numbers except for 2 and 3 are either of the form 6n+1 or 6n-1.
A number of the form 6n+1 can be expressed as 9+25+3(2n-11). The first two numbers are obviously composite. The last is composite whenever 2n-11 is at least 3, so when n is 7 or more. So 43, 49, 55, 61, etc. The highest prime number in this class below 43 is 37.
A number of the form 6n-1 can be expressed as 9+35+3(2n-15). Again the first two numbers are obviously composite. The last is composite whenever 2n-15 is at least 3, so when n is 9 or more. So 53, 59, 65, 71, etc. The highest prime number in this class below 53 is 47.
Therefore the answer is 47.
For completeness, the full list of prime numbers that cannot be expressed as the sum of three positive composite odd numbers is:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 and 47.
Solution of the Week #404 - Points on a Circle
Because triangle ABC is isosceles, and BAC and angle ACB are the same. Draw a line between C and D. Because both BAC and BDC are angles on the same chord, they too are the same.
Triangles BEC and BCD share angle CBD and have another angle in common and are therefore similar.
BC/BE = BD/BC
BD = (BC^2)/BE = 100/4 = 25
Therefore DE = 21.
Interestingly there isn’t enough information to determine the diameter of the circle, but whatever you choose it to be, DE will be equal to 21.