2^a + 2^10 + 2^13 = b^2
a and b are both natural numbers, what are they?
Your Custom Text Here
2^a + 2^10 + 2^13 = b^2
a and b are both natural numbers, what are they?
Choose a value x such that:
You begin with 3x, and round to the closest whole number.
Multiply this by 4x, and round to the closest whole number
Finally multiply this by 5x, and you will have the answer 273.
For example:
Let x = 7/4,
3x = 21/4 = 5.25, round to 5,
Multiply by 4x (7) = 35, round to 35.
Finally multiply by 5x (35/4) to get 306.25
As 306.25 is not 273, this is not the correct value of x. But what is?
Following on from part 1, I have a similar situation, examining the eight distinct points of a nine-point circle of an isosceles triangle.
However, they now form an IRREGULAR octagon. In particular, the two sides of the octagon that meet at the midpoint of the base are one length, and the other six sides are a second length.
Now what is the angle at the apex of the triangle?
(For uniqueness, let the angle be less than 90 degrees).
It is well known that for any triangle, the following nine points:
a) the three midpoints,
b) the three feet of the altitudes (the altitudes are the lines from each vertex to the opposite side, perpendicular to that side),
c) and the three points midway between the vertices and the orthocentre (the orthocentre is the point where the three altitudes cross),
all lie on a circle, known as the Nine-Point Circle.
Sometimes some of those points coincide with one another, for instance the midpoint of the base of an isosceles triangle is also the foot of the altitude from the apex down to the base.
I have an isosceles triangle, and so since two of the nine points coincide, there are now eight distinct points. In my triangle these eight points are equally spaced, forming the vertices of a regular octagon.
What is the angle at the apex of the isosceles triangle?
For bonus points, what is a second possible value for the apex angle?
Using the DDMMYY format, you can change a date to a six digit number, for instance 15th August 2022 would be 150822, and 1st November 2023 would become 011123. Some of these dates can be perfect powers, for instance 11th February 2024 would be 110224, which is 332 squared, and 9th November 2025 would be 091125 which is 45 cubed. You can also make 4th and 5th powers, and also one more beyond that. What is the only date that becomes a power beyond the fifth power?
If Friday 18th April is at the start, what date is at the end?
In a similar vein to my previous puzzle Counter Game, there are a number of counters on the table, but this time you can either remove 2 or 7 of them on each turn. For instance if there were 11 counter there are three solutions: 2,2,7; 2,7,2; 7,2,2; (as before removing 7 then 2 is distinct from removing 2 then 7). Some numbers of counters have no solution, for instance if there are 5 counters you cannot remove them all.
If the number of counters is high enough, there are always more different ways to remove all the counters than to leave one counter behind, but this is not true for some smaller numbers, for instance if there were 12 counters there is only one way of removing them all (2,2,2,2,2,2), but as we have seen, three ways of removing 11 and leaving 1 behind.
What is the highest number of counters, for which there are fewer ways to remove them all than to leave one remaining?
Construct a list of 9 common five-letter words, such that with every new word in the list uses at least one letter that you haven’t used in any of the preceding words. Just to make it a little more difficult, you may only use the letters in the words HUMAN LOGIC.
I have 16 counters. On each turn I either remove 1, 2 or 3 counters until there are no counters left.
I could remove 2 counters eight times, or I could remove five lots of 3 counters then a single counter, or I could remove 3, 2, 2, 1, 3, 1, 1, 1, 1, 1, or any number of different ways.
Well in fact not ‘any’ number of different ways. Your task is to find out exactly how many ways there are. Note: the same combination but occurring in a different order counts as different ways, for instance, there is only one way using 2 eight times, but there are six ways involving five 3s and a 1.
I’ve chosen the number of counters to be 16 because the total number of ways is the square of a prime number. This fact doesn’t particularly help you, except for checking whether or not you are correct.
How many different ways are there?
Within this figure are three squares and three triangles. The edge length of two of the squares is 2 and 3 units respectively. What is the area of the overall shape?

You have probably seen this game going around the interwebz:

The object is to guess the secret word. For each guess you make, you will be told if a letter is correct (green), or if it does occur in the secret word, just not where you’ve placed it (yellow), or if it’s not in the secret word at all (white).
Not one to miss a bandwagon, I thought I’d make a variation on the theme:
In the Wordle below, the letters for the first four guesses are given, and are above the correct column. The puzzle in threefold: firstly reconstruct what the first four guessed words were; secondly, place the four words in the correct order in the grid; thirdly, use the green, yellow and white squares from the first four rows to work out what the actual secret word should be.

Complete the final column to find a secret message:

There are three sisters, all of different ages, but all sharing a birthday.
At some point in the distant past, the older sister’s age was a cube number and her sisters’ ages were both prime numbers.
Now, some time later, the older sister’s age is again a cube number, and the younger sisters’ ages are again both prime numbers.
How old are they all?
In the following sudoku, within each and every 3x3 ‘box’, the rows add up to 9, 15 and 21 and the columns add up to 9, 15 and 21 (in some order).
For instance one box might be:
2 3 4
7 5 9
6 1 8
as the row totals are 9, 21 and 15, and the column totals are 15, 9 and 21.
Other than that, usual sudoku rules apply: the numbers 1 to 9 appear once each in every row, column and box.
Starting tip: list all the possible ways of totalling 9 then look at the central box.

Each row and each column should contain every number from 1 to 6. Additionally, the numbers in each ‘brick’ should add up to a multiple of 3.
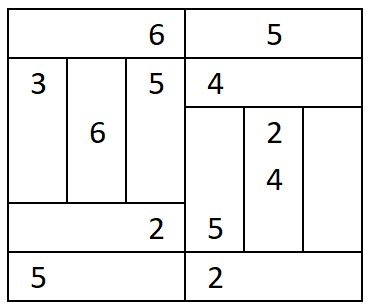
Each row and each column should contain every number from 1 to 6 (1 to 4 in the example). Additionally, each ‘brick’ should contain one even number and one odd number.


There is a building whose plan view is an equilateral triangle, x feet along each side. The building is divided into an internal room and a corridor along two sides of the building, such that the area of the corridor is exactly the same as the area of the internal room. The width of the corridor is sqrt(6x) - sqrt(3x) feet. What is the value of x?

I have taken a regular hendecagon (11-sided polygon) and added extensions to each of the sides so that they intersect as shown. Wherever it is possible to connect two of these intersection points with a horizontal line I have done so, and denoted them A to P. (Except for the magenta dashed line passing through the horizontal side of the hendecagon, which has several intersection points on it, but can be ignored for the purposes of this puzzle).
Some of these lines A to P have a very curious property, that if you form a circle whose diameter exactly coincides with said line, the circle will pass exactly through the midpoints of two of the sides of the original hendecagon.
Can you list all those lines which have this property?

There are two ways to draw a rectangle whose length is twice as long as its width, within a quarter circle of radius 1, such that all four corners lie on the boundary of the quarter circle.
One of the rectangles has an area greater than the other, but by how much exactly?

What is the value of the following sum?
1/4 + 1/10 + 1/18+ 1/28 + … continuing forever,
where each denominator is each successive natural number, n, multiplied by n+3.