From the first part:
F+S=65
F=65-S
From the second part:
F=3*(S-(F-S))
F=6S-3F
2F=3S
Combining:
130-2S=3S
5S=130
S=26, F=39
Fred is 39, Sally is 26
Your Custom Text Here
From the first part:
F+S=65
F=65-S
From the second part:
F=3*(S-(F-S))
F=6S-3F
2F=3S
Combining:
130-2S=3S
5S=130
S=26, F=39
Fred is 39, Sally is 26


A systematic approach might be to note that the centre will lie on the perpendicular bisector of any chord. Since we know the position of three points on the circle, we can construct chords from pairs of those and use coordinate geometry to find the centre.
MEME
BANANA
SEAHORSE
TANTAMOUNT
IDIOSYNCRASY
For the GCD to be 7, a necessary condition is that the two numbers are divisible by 7. This of course means that not only are abc and cba divisible by 7, but so is abc-cba.
abc = 100a+10b+c and cba = 100c+10b+a, so their difference is 99a-99c, or 99(a-c).
Since 99 is not a multiple of 7, (a-c) must be, so a and c must differ by 7 (they can’t be identical, since the GCD of aba and aba is aba).
Since they are single digits, they could only be: (0,7), (1,8) or (2,9).
For each case we can find the middle digit or digits b that makes abc (and therefore also cba) a multiple of 7.
This leads us to 007,700; 077,770; 168,861; and 259,952.
We can rule out 007,700 and 077,770 on the basis that 007 and 077 are not three-digit numbers.
The third pair 168 and 861 are also both divisible by 3 and therefore have a GCD of 21.
The final pair of 259 and 952 are therefore the numbers we are looking for. 259 = 7x37 and 952 = 7x8x17.
(a^7)*b-a*(b^7)
Let’s start by plugging a couple of numbers into the expression. When a,b is 2,1 it computes to 126, and when a,b is 3,1 it computes to 2184. These two numbers have a GCD of 42, so we have an upper bound, but will the expression ALWAYS come out to a multiple of 42 for any integers a,b? 42 is 2x3x7, so we can separately look at whether the expression is always a multiple of 2,3 and 7.
To help us we can factorise the expression thusly:
ab(a^6-b^6)
difference of squares
ab(a^3+b^3)(a^3-b^3)
sum/difference of cubes:
ab(a+b)(a-b)(a^2+ab+b^2)(a^2-ab+b^2)
Unfortunately we can’t break it down any further than that.
Looking at whether the expression is always even is straightforward. If either a or b is even then the whole expression will be, but if they’re both odd, the term (a-b) will be even.
As to divisibility by 3, again if either a or b is, then the whole thing is. If a and b have the same remainder after dividing by 3, then (a-b) will be divisible by 3, and if they differ (1 and 2), then (a+b) will be divisible by 3.
Finally looking at divisibility by 7 is a bit more complicated.
We can make a table of all of the possibilities of remainders after dividing by 7 (the modulo), to see what we can determine:

As before if either a or b is 0, the whole expression is divisible by 7, and also if a=b or if a+b=7 (using the (a-b) and (a+b) factors).
Unfortunately for the remaining cases we need to use the messier factors. Lets assume b=1 and let a=2,3,4,5:
(a^2+a+1)=7,13,21,31 and (a^2-a+1)=1,7,13,21
So between the two factors one will always be divisible by 7 if b=1. That just places four more xs into the grid. However, since the expressions are symmetrical with respect to a and b, we can also put xs in the column where a=1. Also since the two factors differ only in the sign of the middle term, we can regard b=6 as b=-1, and a=6 as a=-1 and check off those cases too:

Finally allowing b=2 and a=3,4
(a^2+2a+4)=19,28 and (a^2-2a+4)=7,12
We can place xs in the remaining spots in row b=2, and by symmetry, the other six spots too.

So therefore (a^7)*b-a*(b^7) is always divisible by 2,3 and 7, and so the ultimate answer is 42.
If you add more squares to form a repeated tiling, it becomes clear that the area of the triangle is half that of the blue square. The area of the blue square is the sum of the areas of the two original squares, by Pythagoras, so therefore the area of the red triangle is the mean average of the area of the two original squares.


The fractional part x-a will necessarily be less than 1, and so if we want to maximise x, we should use our highest number as a, so a=7. To maximise the fractional part (x-a) we need to minimise b+1/(c+1/d), and so we should use our smallest possible value for b, so b=1. Then c should be the larger of what is left, c=5, and so d=4.
Then working backwards to evaluate the fraction:
x=7+1/(1+1/(5+1/4))
x=7+1/(1+4/21)
x=7+21/25
x=7.84
They can all be followed by a pair of consecutive letters of the alphabet to form a six-letter word:
SCARAB THOUGH NAPALM SOLEMN TECHNO DOLLOP DIVERS DIVEST GALAXY
They are placed in order according to the letters that have been added.
Of the four words in the second list, one can also be followed by a pair of consecutive letters: PARA -> PARADE, and therefore belongs between SCAR and THOU in the list.
The other three could be followed by a pair of consecutive letters in reverse order: BECKON, CLEFTS, PASTED.
Both scales are linear, so we can (mentally) draw straight lines between the data points given in the question, but we currently have two lines to think about, the Fahrenheit and Celsius. However since we are only interested in the point where they are positive and negative by the exact same amount, we can think of a single line which is the average of the two (or the sum of the two would also work), and find the point where it equals 0.
So we have 16 for the first data point and -40 for the second. If we mentally split that into seven ‘chunks’ of 8 degrees each, we can see that we want to be 2 chunks away from the point where Celsius is 0, where 7 chunks would get all the way to -40. So Celsius will be 2/7 * -40, or -80/7, which is -11 3/7 degrees. Predictably, at that point, Fahrenheit will be 11 3/7 degrees.

Calling the radius of the top left circle ‘r’, and the missing length we seek ‘x’, we can work our way around the rectangle, and express each of the radii in terms of r and x. We can form two right angles triangles and form their Pythagorean equations as below:
(1) x^2+(3-r)^2=(3+x-3r)^2
(2) x^2+r^2=(6-x-3r)^2
Taking the difference of these two, the x^2 terms cancel:
(3-r)^2-r^2=(3+x-3r)^2-(6-x-3r)^2
Factoring each side as a difference of squares:
(3-2r)(3)=(3+x-3r-6+x+3r)(3+x-3r+6-x-3r)
(9-6r)=(-3+2x)(9-6r)
If (9-6r)=0, r=3/2, but that would mean the top right circle would disappear entirely, so that’s not possible.
Since (9-6r) is not equal to 0, we can divide both sides by it:
1=(-3+2x)
4=2x
x=2
And that’s the answer!
One part is obvious: that the initial digit increases with each term, so the missing term will start with a 6. The other part is that the product of the digits of each number is the same number but with the initial digit omitted, eg 4x3x8x4=384. Specifically each term is the smallest it could be (excluding the use of 0). So the missing term will be 612.
11, 236, 315, 4384, 5175, 612, 7735, 8128, 9135
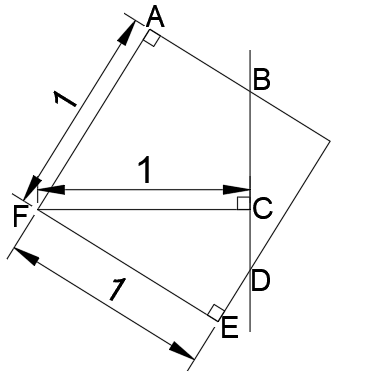
The above figure represents one of the 1x1 squares, and how it interacts with the edge of the 3x3 square represented by the line through BD. Because of the fact that the inner point of the square F lies on a corner of the middle square of the figure we can say that FC is equal to 1 in length. ABCF is a kite, and therefore AB=BC. Likewise CDEF is a kite, and so CD=DE. The overall change to the perimeter from this square is that we lose BD, but gain AB, DE, AF and FE. But BD is just AB+DE so they cancel out, and AF=FE=1, so overall we gain 2. Since there are four such squares, we gain 8 compared to the original 3x3 square which has a perimeter of 12. And so therefore the overall perimeter = 20.
There’s likely a more elegant way of doing this, but this was my approach. I’ve rotated the figure and put in place a coordinate system with the origin at the centre of the lower left circle. Without loss of generality I’m using unit circles. By Pythagoras the top right circle is at (10,0) as part of a 3,4,5 triangle. Since the distance between adjacent circles is 2, and we know the triangles formed with the horizontal are in the ratio 3,4,5, we can easily find the coordinates of the circles next to the origin circle, and by extension, any circle we wish. The red line is the critical line that goes from (0,1) to (10,1). The first two circles it passes through are centred 0.6 off the line. The third circle is indeed tangent as appears from the figure. The other two circles it passes through are centred 0.2 off the line. Using Pythagoras we can find the lengths of the chords to be 1.6 and 0.8*sqrt(6) respectively. The overall proportion then is 4/25(2+sqrt(6)) or just under 0.72.

After each guess, the player is told whether each individual letter in that position in the word is earlier or later in the alphabet than the guessed letter.
After three guesses she knew the first letter was C-H, the second A-H, the third E-R, the fourth A-D and the final letter U-Z. DELAY obviously fits this, along with some other possibilities such as FANCY, which I hid in plain sight in the question.
I based this puzzle on the game ‘Wordle Peaks’ which I play every day. You can find it at: https://vegeta897.github.io/word-peaks/
For the solution below I have started with a large rhombus, then three large kites from left to right, leaving a scalene triangle. I have then constructed the incircle of that triangle and drawn lines from the incentre to meet the three sides of the triangle at right angles, forming the final three kites. Upon inspection, all seven kites are different in both size and shape.

Start by drawing a semicircle whose diameter is on the short side of the rectangle. Draw a line tangent to this semicircle from one of the far vertices, dividing the rectangle into a triangle and a quadrilateral. Draw the incircle of the triangle. Draw lines from the centre of the incircle to each of the three points where the incircle touches the triangle. Draw a line from the centre of the semicircle to the point where the tangent line touches the semicircle. Et voila, a square and four different kites.

There is a special case when the ratio of the sides of the rectangle is (1+sqrt(2))/2, when the upper and left kites are identical. We avoid this problem by drawing the semicircle on the long side instead in that case. Another special case is when the rectangle is a square, when the lower left and mid left kites are identical. This cannot be avoided by using the other side of the square, which is why the rectangle was specified in the question as non-square.
By the way, it’s a nice little fact that the largest kite, the right one in the diagram, will always be exactly half the area of the overall rectangle.
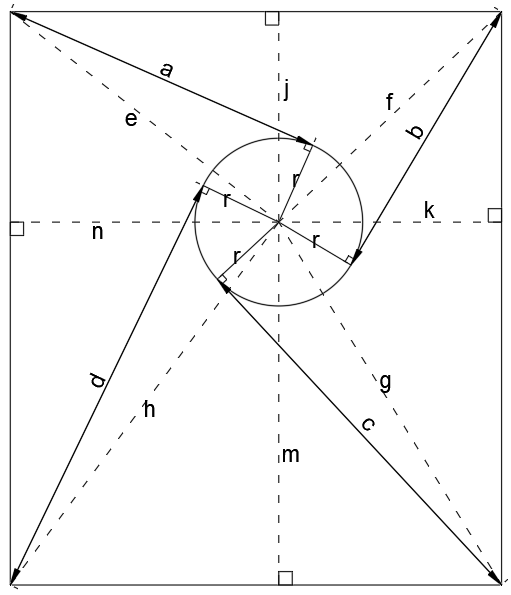
Looking at the general case above, each tangent line a,b,c,d is by definition at right angles to the radius of the circle, r, so we can define a,b,c,d in terms of e,f,g,h,r using Pythagoras:
a^2=e^2-r^2
b^2=f^2-r^2
c^2=g^2-r^2
d^2=h^2-r^2
We can then also define e,f,g,h in terms of the perpendicular distances from the centre of the circle to the edges of the rectangle j,k,m,n:
e^2=j^2+n^2
f^2=j^2+k^2
g^2=k^2+m^2
h^2=m^2+n^2
Next I’m going to use the above to find an expression for a^2+c^2:
a^2+c^2=j^2+n^2+k^2+m^2-2r^2
And also for b^2+c^2:
b^2+d^2=j^2+k^2+m^2+n^2-2r^2
Both these are equal to the same thing, so a^2+c^2=b^2+d^2
Returning to the numbers in the puzzle:
10^2+15^2=6^2+?^2
?^2=289
?=17
In 1990, Leoni 29, Joshua 11.
In 2024, Leoni 63, Joshua 45.

We can place two pairs of similar triangles within the shape as shown above. The red triangles are clearly in the ratio of 3,4,5. It’s less obvious what the ratio of the sides of the blue triangles is, until you construct a grid as below which demonstrates that if you want to add an angle to the small angle of a 3,4 right triangle to total 45 degrees, that new triangle will have legs in the ratio of 7 to 1. (This generalises to a triangle with legs a,b pairing with a triangle with legs a+b,|a-b|).

So c/b=7, c/a=4/3 and a+b=1. From this we can work out that a=21/25, b=4/25 and c=28/25. By Pythagoras, d is therefore 4/5*sqrt(2). By similar triangles, e/5=c/d, so e=7/2*sqrt(2).
Since the triangle is right-angled and isosceles, its area is ((d+e)^2)/2, which equals exactly 18.49.